카이제곱 검정: 범주형 변수 간 관계 심층 분석 입문

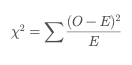
카이제곱 검정: 범주형 변수 간 관계 심층 분석 입문

핵심 기술: 본 콘텐츠는 두 범주형 변수 간의 통계적 독립성(관계 유무)을 검정하는 카이제곱 검정(Chi-squared test)의 기본 원리, 적용 방법 및 해석 과정을 상세하게 다룹니다. 데이터 분석에서 필수적인 가설 검정 기법 중 하나인 카이제곱 검정을 통해 데이터의 패턴을 이해하고 의미 있는 인사이트를 도출하는 방법을 소개합니다.

기술적 세부사항:

• 정의 및 목적:
  • 두 범주형 변수 간의 관련성(독립성)을 검정하는 통계 기법입니다.
  • 관측된 빈도와 기대되는 빈도 간의 차이가 우연인지 통계적으로 유의미한지 판단합니다.
• 적용 대상: 성별과 구매 여부, 직업군과 질병 발생률 등 두 개의 범주형 변수 간의 관계를 분석할 때 사용됩니다.
• 가설 설정:
  • 귀무가설 (H0): 두 변수는 서로 독립적입니다 (관계가 없습니다).
  • 대립가설 (H1): 두 변수는 서로 독립이 아닙니다 (관계가 있습니다).
• 핵심 통계량 (χ²):
  • χ² = Σ [ (관측 빈도 - 기대 빈도)² / 기대 빈도 ]
  • 관측된 데이터와 이론적으로 기대되는 데이터 간의 차이를 정량화합니다.
  • χ² 값이 클수록 관측 결과가 기대와 다름을 의미하며, 귀무가설 기각 가능성이 높아집니다.
• 기대 빈도 (Expected Frequency):
  • 두 변수가 독립이라고 가정했을 때 각 경우(조합)에서 예상되는 빈도입니다.
  • 계산 예시: 전체 인원 x (행 합계 / 전체 합계) x (열 합계 / 전체 합계) (이는 더 직접적인 계산법이 존재하며, 문서에서는 간략히 설명되었습니다. 실제로는 행/열 비율을 사용하여 계산합니다.)
• 자유도 (Degrees of Freedom, df):
  • 카이제곱 분포의 모양을 결정하는 요소입니다.
  • df = (행 개수 - 1) × (열 개수 - 1)
• p-value:
  • 귀무가설이 참이라고 가정했을 때, 관측된 결과 또는 그보다 극단적인 결과가 우연히 발생할 확률입니다.
  • 해석 기준: p < 0.05 이면 귀무가설 기각 (두 변수는 관련 있음). p ≥ 0.05 이면 귀무가설 채택 (두 변수는 독립).

개발 임팩트:
카이제곱 검정을 통해 데이터 내 숨겨진 패턴과 변수 간의 유의미한 관계를 통계적으로 규명할 수 있습니다. 이는 사용자 행동 분석, A/B 테스트 결과 해석, 특정 그룹의 특성 파악 등 다양한 데이터 기반 의사결정에 활용되어 서비스 개선 및 비즈니스 성과 향상에 기여합니다.

커뮤니티 반응:
(제공된 원문에는 커뮤니티 반응에 대한 언급이 없습니다.)

톤앤매너: 이 콘텐츠는 학습자의 입장에서 어려운 통계 개념을 쉽게 이해할 수 있도록 친절하고 명확한 설명을 제공하는 데 중점을 두고 있으며, IT 실무 맥락에서 카이제곱 검정의 유용성을 강조합니다.