적록색약자를 위한 그림 영역 분할: DFS 알고리즘 활용 실습

핵심 기술

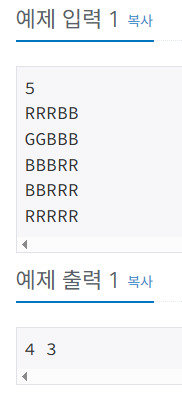
본 콘텐츠는 NxN 크기의 색칠된 그림에서 정상인과 적록색약자가 인식하는 영역 수를 계산하는 문제를 깊이 우선 탐색(DFS) 알고리즘을 활용하여 해결하는 방법을 다룹니다. 적록색약자의 경우 빨간색(R)과 초록색(G)을 동일한 색으로 간주하는 특성을 반영하여 영역을 구분하는 것이 핵심입니다.

기술적 세부사항

• 문제 정의: NxN 격자 형태의 색칠된 그림에서 R, G, B 세 가지 색으로 구분되며, 상하좌우로 연결된 같은 색상의 셀들이 하나의 영역을 이룰 때, 정상인과 적록색약자가 인식하는 영역 수를 각각 계산합니다.
• 알고리즘: 깊이 우선 탐색(DFS) 알고리즘을 사용하여 연결된 영역을 탐색합니다.
• 정상인 탐색: 방문하지 않은 좌표에서 시작하여 같은 색상으로 연결된 모든 셀을 탐색하고, 탐색이 완료될 때마다 영역 카운트를 1씩 증가시킵니다. visited 배열을 사용하여 이미 탐색한 셀은 다시 방문하지 않도록 처리합니다.
• 적록색약 탐색: visited 배열을 초기화한 후, DFS 탐색 시 색상 비교 로직을 수정합니다. 적록색약자는 R과 G를 같은 색으로 인식하므로, 현재 셀의 색상이 R 또는 G이고 탐색할 인접 셀의 색상 역시 R 또는 G일 경우 같은 영역으로 간주하여 탐색을 계속합니다. 또한, R/G와 동일한 색상이 아닌 다른 단일 색상(color == grid[nx][ny])일 경우에도 탐색을 지속합니다.
• 구현: dx, dy 배열을 활용하여 상하좌우 인접 좌표를 효율적으로 탐색하며, 재귀 호출을 통해 연결된 모든 영역을 탐색합니다.

개발 임팩트

• 그래프 탐색 알고리즘(DFS)에 대한 이해도를 높일 수 있습니다.
• 실제적인 문제 해결 능력과 알고리즘 설계 능력을 향상시킬 수 있습니다.
• 다양한 조건(예: 색맹)에 따른 알고리즘 수정 및 적용 능력을 배양할 수 있습니다.
• 코딩 테스트나 알고리즘 문제 해결 시 유사한 문제에 대한 접근 방식을 익힐 수 있습니다.

커뮤니티 반응

톤앤매너

기술적으로 정확하고 명확한 설명으로, 알고리즘 학습자에게 실질적인 도움을 제공합니다. 코드를 분석하며 단계별로 문제를 해결하는 방식을 제시합니다.