동적 계획법(DP) 이해하기: 피보나치 수열 예제를 통한 메모이제이션과 반복문 접근법 비교 분석

핵심 기술

동적 계획법(DP)은 큰 문제를 여러 개의 작은 하위 문제로 나누고, 이 하위 문제들의 해결책을 저장해두고 재활용하여 효율적으로 문제를 해결하는 프로그래밍 기법입니다.

기술적 세부사항

• DP 기본 원리: 큰 문제를 작은 문제로 분해하고, 중복되는 하위 문제의 해를 저장 및 재사용.
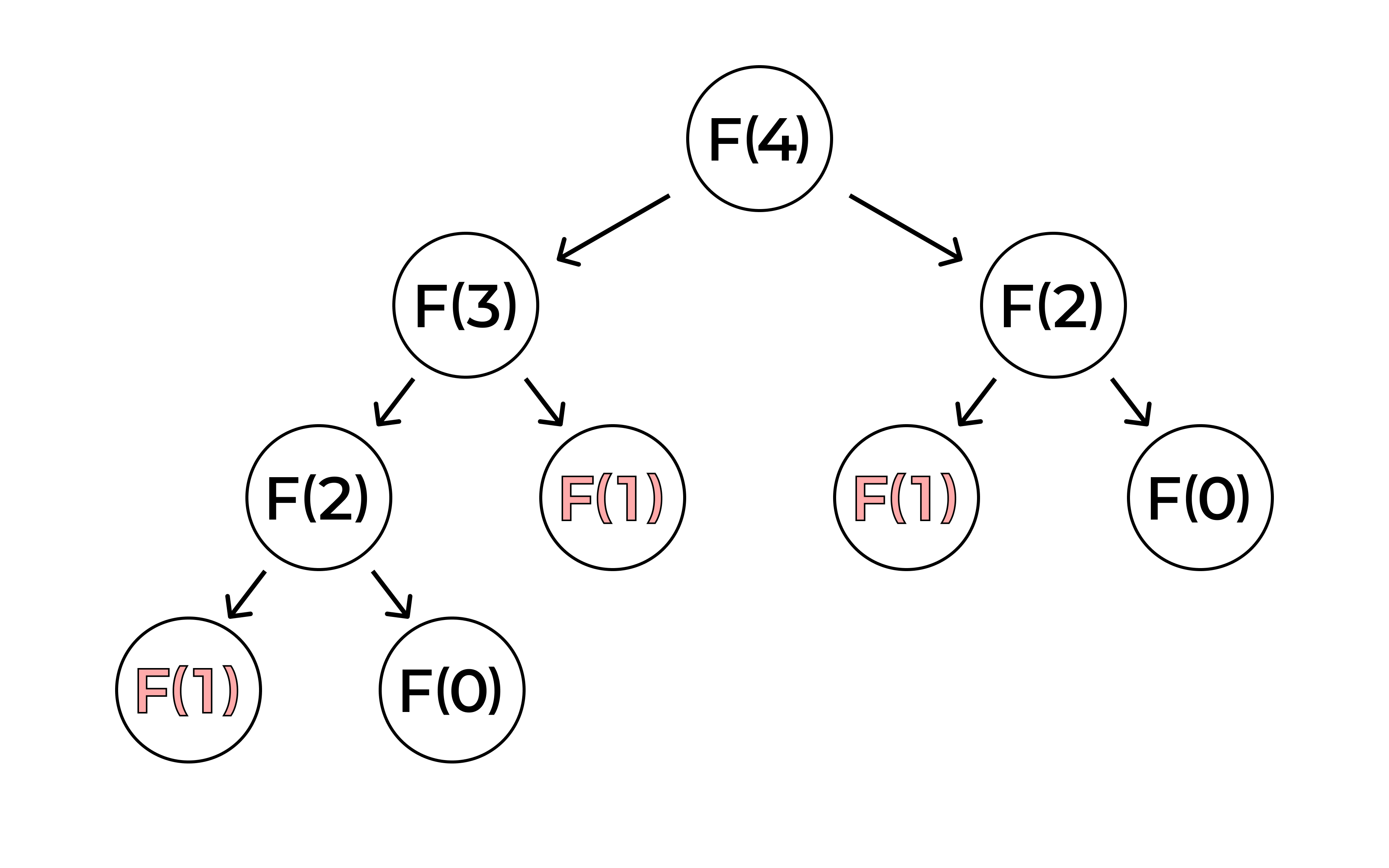
• 피보나치 수열 예제: DP 적용을 위한 대표적인 예시로, F(n) = F(n-1) + F(n-2) 규칙을 가짐.
• 중복 호출 문제: 피보나치 수열 계산 시 동일한 하위 문제가 반복적으로 호출되어 비효율 발생.
• 메모이제이션 (Top-Down):
  • 재귀 호출 방식으로, 계산된 결과는 딕셔너리 등에 저장(memoization).
  • 같은 하위 문제가 다시 호출될 때 저장된 값을 반환하여 중복 계산 방지.
  • 장점: 코드가 직관적이고 이해하기 쉬움, 꼭 필요한 계산만 수행.
  • 단점: 재귀 깊이가 깊어질 경우 스택 오버플로우 위험, 함수 호출 오버헤드.
  • 예제 코드: fib_memo(n, memo) 함수.
• 반복문 접근법 (Bottom-Up):
  • 가장 작은 하위 문제부터 시작하여 점진적으로 더 큰 문제의 해를 계산.
  • 배열(dp 테이블)을 사용하여 하위 문제의 결과 저장.
  • 장점: 스택 오버플로우 위험 없음, 실행 속도가 빠름, 문제 해결 과정이 명확.
  • 단점: 모든 하위 문제를 계산할 수 있어 불필요한 계산 발생 가능, 코드 길이가 길어질 수 있음.
  • 예제 코드: fib_bottom_up(n) 함수.
• 추천 문제: 피보나치 수, 피보나치 함수, 1, 2, 3 더하기, 2xN 타일링, 1로 만들기, 쉬운 계단 수, 계단 오르기 등 DP 구조 익히기 및 응용 문제.

개발 임팩트

• 알고리즘의 시간 복잡도를 크게 개선하여 대규모 데이터 처리 시 성능 향상.
• 복잡한 문제를 체계적으로 분석하고 해결하는 능력 배양.
• 코딩 테스트 및 알고리즘 경진대회에서의 문제 해결 능력 강화.

커뮤니티 반응

(원문에서 커뮤니티 반응에 대한 직접적인 언급은 없으나, DP는 CS 교육 과정 및 코딩 테스트에서 매우 중요하게 다루어지는 주제로, 관련 온라인 강의, 블로그, 커뮤니티에서 활발히 논의되고 학습 자료가 공유됨.)