그래디언트 방법을 사용한 2변수 함수의 극값 계산 방법
카테고리
프로그래밍/소프트웨어 개발
서브카테고리
데이터 분석
대상자
- 대상자: Python 개발자, 데이터 과학자, 기계 학습 엔지니어
- 난이도: 중급 이상 (수학적 기초와 Python 라이브러리 사용 경험이 필요)
핵심 요약
- 그래디언트 방법: 함수의 극값을 찾기 위해 기울기(gradient)를 따라 이동하는 알고리즘으로, 다변수 함수의 편도함수를 계산하여 사용
- 핵심 구현:
numpy와matplotlib사용, 편도함수 계산 및 알파(alpha) 파라미터 조정 - 알파(alpha) 값: 너무 크면 근처 극값을 놓칠 수 있고, 너무 작으면 계산 속도가 느려짐 (예:
alpha = 0.01)
섹션별 세부 요약
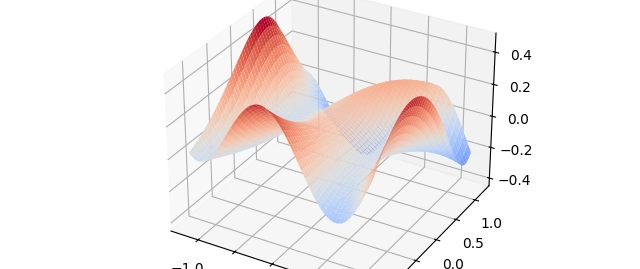
1. 함수 정의 및 그래프 시각화
- 함수 정의:
```python
def f(x, y):
return np.sin(1/2 x2 - 1/4 y2 + 3) np.cos(2x + 1 - np.exp(y))
```
- 그래프 생성:
numpy.meshgrid와matplotlib을 사용해 3D 표면 그래프 생성 - 필요 라이브러리:
matplotlib,numpy설치 및 임포트
2. 편도함수 계산
- 편도함수 정의:
- ∂f/∂x: y를 상수로 고정하고 x에 대해 미분
- ∂f/∂y: x를 상수로 고정하고 y에 대해 미분
- 예시:
```python
f(x, y) = x² + xy + 3x → ∂f/∂x = 2x + y + 3, ∂f/∂y = x
```
- Python 구현:
lambda함수를 사용한 편도함수 자동 계산
3. 그래디언트 알고리즘 구현
- 알고리즘 핵심:
- 점 이동 공식:
```python
xB = xA + α * ∂f/∂x(xA, yA)
yB = yA + α * ∂f/∂y(xA, yA)
```
- 수렴 조건: epsilon 값으로 좌표 변화가 충분히 작아졌는지 확인
- 알파(alpha) 조정: 극값 탐색 효율성에 따라 실험적 최적화 필요
4. 글로벌 극값 탐색
- 로컬 극값 한계: 시작점에 따라 로컬 극값만 찾을 수 있음
- 글로벌 극값 탐색 방법:
- 그리드 탐색: numpy.linspace로 생성된 그리드 포인트에서 알고리즘 반복 수행
- 랜덤 포인트: 다수의 무작위 시작점을 사용해 최대값 비교
결론
- 실무 팁:
- alpha 값을 0.01로 설정하여 극값 탐색 효율성 균형 유지
- 글로벌 극값을 찾기 위해: 그리드 탐색 또는 다수의 시작점 사용
- matplotlib로 결과 시각화하여 극값 위치 확인 가능
- 핵심 구현 요소:
numpy와matplotlib사용, 편도함수 계산, 수렴 조건 설정