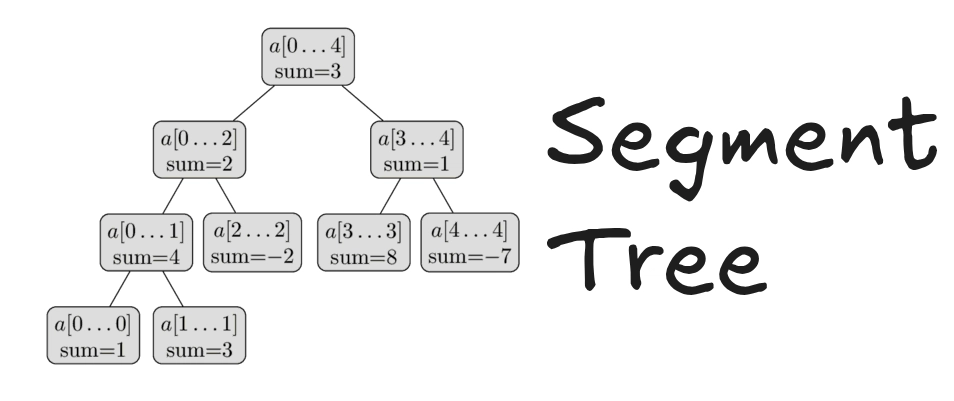
세그먼트 트리

카테고리

프로그래밍/소프트웨어 개발

서브카테고리

데이터 분석

대상자

• 소프트웨어 개발자 및 알고리즘 개발자에게 유용
• 중간~고급 수준의 이해가 필요 (트리 구조 및 알고리즘 기본 지식 필요)

핵심 요약

• 세그먼트 트리는 배열의 구간(범위)에 대한 정보를 트리 구조로 저장하여 O(log n) 시간 내 범위 쿼리 및 점 업데이트 가능
• 루트는 전체 배열 범위, 리프 노드는 개별 요소를 표현
• C++ 구현 예시에서 SegmentTree 클래스는 build(), queryUtil(), update() 메서드를 포함

섹션별 세부 요약

1. 세그먼트 트리 정의 및 목적

• 범위 쿼리 (예: 합, 최소값, 최대값)과 점 업데이트를 효율적으로 처리
• 브루트 포스 대비 O(log n) 시간 복잡도로 성능 향상
• 트리 구조로 배열의 구간을 표현 (루트: 전체, 리프: 개별 요소)

2. 구조 및 예시

• 트리 노드는 각각 특정 구간의 합을 저장
• 예시 배열 [2, 4, 5, 7, 8, 9]의 세그먼트 트리 구조:

- 루트: [0,5]

- 자식 노드: [0,2], [3,5]

- 리프 노드: [0,0], [1,1], ...

3. C++ 구현 예시

• SegmentTree 클래스 정의:

- build() 메서드: 배열을 기반으로 트리 생성

- queryUtil() 메서드: 특정 범위의 합 계산

- update() 메서드: 특정 인덱스의 값 업데이트

• 시간 복잡도:

- Build: O(n)

- Query: O(log n)

- Update: O(log n)

결론

• 범위 쿼리와 점 업데이트가 동시에 필요한 경우 세그먼트 트리를 사용하는 것이 효율적
• C++ 구현 예시에서 SegmentTree 클래스를 참고하여 실무에 적용 가능